Was ist ein ANOVA-Test? Definition, Typen, Beispiele

Haben Sie sich jemals gefragt, wie Forscher feststellen, ob verschiedene Gruppen in einer Studie signifikant unterschiedliche Ergebnisse haben? Die Varianzanalyse, allgemein bekannt als ANOVA, ist eine statistische Methode, die bei der Beantwortung dieser wichtigen Frage hilft. Ob beim Vergleich der Wirksamkeit verschiedener Behandlungen, beim Verständnis der Auswirkungen verschiedener Lehrmethoden oder bei der Bewertung von Marketingstrategien - die ANOVA ist ein leistungsfähiges Instrument, mit dem wir die Mittelwerte von drei oder mehr Gruppen vergleichen können, um festzustellen, ob mindestens eine Gruppe signifikant unterschiedlich ist.

Dieser Leitfaden führt Sie durch die grundlegenden Konzepte, mathematischen Grundlagen, Typen und praktischen Anwendungen der ANOVA und stellt sicher, dass Sie verstehen, wie Sie Experimente planen, Annahmen überprüfen, Analysen durchführen und Ergebnisse effektiv interpretieren können. Am Ende werden Sie sehen, warum die ANOVA ein Eckpfeiler der statistischen Analyse in zahlreichen Bereichen ist und einen robusten Rahmen für fundierte Entscheidungen auf der Grundlage von Daten bietet.

Was ist ANOVA?

Die ANOVA oder Varianzanalyse ist eine statistische Methode, mit der die Mittelwerte von drei oder mehr Gruppen verglichen werden, um festzustellen, ob sich mindestens eine von ihnen signifikant von den anderen unterscheidet. Mit dieser Technik lässt sich feststellen, ob beobachtete Unterschiede in den Stichprobenmittelwerten auf tatsächliche Unterschiede in den Populationsmittelwerten zurückzuführen sind oder lediglich das Ergebnis zufälliger Schwankungen sind.

Zweck der ANOVA

1. Vergleich mehrerer Gruppen: Mit der ANOVA können Sie gleichzeitig die Mittelwerte von drei oder mehr unabhängigen Gruppen vergleichen. Dies ist effizienter und aussagekräftiger als die Durchführung mehrerer t-Tests, bei denen das Risiko eines Fehlers vom Typ I (falsch positive Ergebnisse) steigt.
2. Identifizierung signifikanter Unterschiede: Durch den Test auf Unterschiede in den Gruppenmittelwerten hilft die ANOVA festzustellen, ob sich eine der Gruppen signifikant voneinander unterscheidet. Dies ist wichtig bei Experimenten, bei denen Behandlungen oder Interventionen verglichen werden.
3. Aufteilung der Varianz: Die ANOVA teilt die in den Daten beobachtete Gesamtvarianz in Varianz zwischen Gruppen und Varianz innerhalb von Gruppen auf. Dies hilft dabei, die Quellen der Variabilität in den Daten zu verstehen.
4. Auswertung von Wechselwirkungen: Mit der zweiseitigen ANOVA können Wechselwirkungen zwischen den Faktoren bewertet werden. Das bedeutet, dass Sie sehen können, ob die Wirkung eines Faktors von der Höhe eines anderen Faktors abhängt.
5. Leitfaden für weitere Analysen: Wenn die ANOVA signifikante Unterschiede aufzeigt, führt dies häufig zu weiteren Analysen, z. B. Post-hoc-Tests, um festzustellen, welche Gruppen sich voneinander unterscheiden.

Bedeutung der ANOVA in der statistischen Analyse

Die ANOVA ist ein Eckpfeiler der statistischen Analyse in vielen Bereichen, darunter Psychologie, Medizin, Landwirtschaft, Marketing und Bildung. Ihre Bedeutung liegt in ihrer Vielseitigkeit und Robustheit beim Vergleich mehrerer Gruppen und beim Verständnis komplexer Datenstrukturen.

• Erhöhte Genauigkeit: Die ANOVA kontrolliert die Fehlerrate vom Typ I besser als mehrere t-Tests und liefert somit zuverlässigere Ergebnisse beim Vergleich mehrerer Gruppen.
• Umfassende Analyse: Sie bietet einen systematischen Ansatz zum Verständnis der Variabilität von Daten, indem sie die Gesamtvarianz in sinnvolle Komponenten zerlegt.
• Flexibel: Die ANOVA kann mit verschiedenen Versuchsplänen umgehen, einschließlich Einweg-, Zweiweg- und multivariaten Versuchsplänen, wodurch sie an verschiedene Forschungsfragen und Datenstrukturen angepasst werden kann.
• Einblicke in Wechselwirkungen: Durch die Bewertung von Wechselwirkungen zwischen Faktoren bietet die ANOVA tiefere Einblicke in die Art und Weise, wie verschiedene Variablen gemeinsam das Ergebnis beeinflussen.
• Grundlage für fortgeschrittene Methoden: Die ANOVA bildet die Grundlage für komplexere statistische Methoden wie MANOVA (Multivariate ANOVA), ANCOVA (Analyse der Kovarianz) und ANOVA mit wiederholten Messungen, die für die Analyse komplexerer Datensätze unerlässlich sind.
• Weitverbreitete Anwendung: Die Prinzipien der ANOVA werden in vielen verschiedenen Disziplinen angewandt, was sie zu einem grundlegenden Werkzeug für Forscher und Analysten macht, die aussagekräftige Schlussfolgerungen aus ihren Daten ziehen wollen.

ANOVA Mathematische Grundlagen

Die ANOVA basiert auf mehreren mathematischen Schlüsselkonzepten. Ein solides Verständnis dieser Grundlagen wird Ihr Verständnis vertiefen und Ihre Fähigkeit, die ANOVA effektiv anzuwenden, verbessern.

Verstehen der Varianz und ihrer Komponenten

Die Varianz misst, wie stark sich die Datenpunkte in einem Satz vom Mittelwert des Satzes unterscheiden. Sie ist für die ANOVA von entscheidender Bedeutung, da die Technik auf der Aufteilung dieser Varianz beruht, um Unterschiede zwischen Gruppen zu verstehen.

• Gesamtvarianz: Die Gesamtvariabilität in den Daten.
• Zwischen-Gruppen-Varianz: Die Variabilität aufgrund der Unterschiede zwischen den Gruppenmitteln.
• Varianz innerhalb der Gruppe: Die Variabilität innerhalb jeder Gruppe.

Zur Veranschaulichung: Stellen Sie sich vor, Sie haben Testergebnisse von drei verschiedenen Klassen. Die Gesamtvarianz umfasst alle Punktwertvariationen, aber die Varianz zwischen den Gruppen konzentriert sich auf die Unterschiede zwischen den durchschnittlichen Punktwerten der Klassen, und die Varianz innerhalb der Gruppe betrachtet die Streuung der Punktwerte innerhalb jeder Klasse.

Formeln und Berechnungen

Der Kern der ANOVA liegt in der Berechnung des F-Verhältnisses, das die Varianz zwischen den Gruppen mit der Varianz innerhalb der Gruppen vergleicht.

ANOVA-Berechnung

1. Berechnen Sie die Gruppenmittelwerte: Berechnen Sie den Mittelwert für jede Gruppe.
2. Gesamtmittelwert: Berechnen Sie den Mittelwert aller Datenpunkte zusammen.
   
   X_Gesamt = (ΣX_i) / n
3. Summe der Quadrate zwischen (SSB): Damit wird die Variation aufgrund der Wechselwirkung zwischen den Gruppen gemessen.
   
   SSB = Σ (n_j * (X_j - X_total)^2)
   Dabei ist n_j die Anzahl der Beobachtungen in Gruppe j, X_j ist der Mittelwert von Gruppe j und k ist die Anzahl der Gruppen.
4. Summe der Quadrate innerhalb (SSW): Damit wird die Variation innerhalb jeder Gruppe gemessen.
   
   SSW = Σ Σ (X_ij - X_j)^2
   Dabei ist X_ij die Beobachtung i in Gruppe j.
5. Freiheitsgrade: Berechnen Sie die Freiheitsgrade für zwischen den Gruppen (dfB) und innerhalb der Gruppen (dfW).
   
   dfB = k - 1
   dfW = N - k
   Dabei ist N die Gesamtzahl der Beobachtungen.
6. Mittlere Quadrate: Berechnen Sie die mittleren Quadrate für zwischen den Gruppen (MSB) und innerhalb der Gruppen (MSW).
   
   MSB = SSB / dfB
   MSW = SSW / dfW
7. F-Quotient: Berechnen Sie schließlich den F-Quotienten.
   
   F = MSB / MSW

Der F-Quotient gibt an, ob die Varianz zwischen den Gruppen signifikant größer ist als die Varianz innerhalb der Gruppen, was auf signifikante Unterschiede zwischen den Gruppenmitteln hinweist.

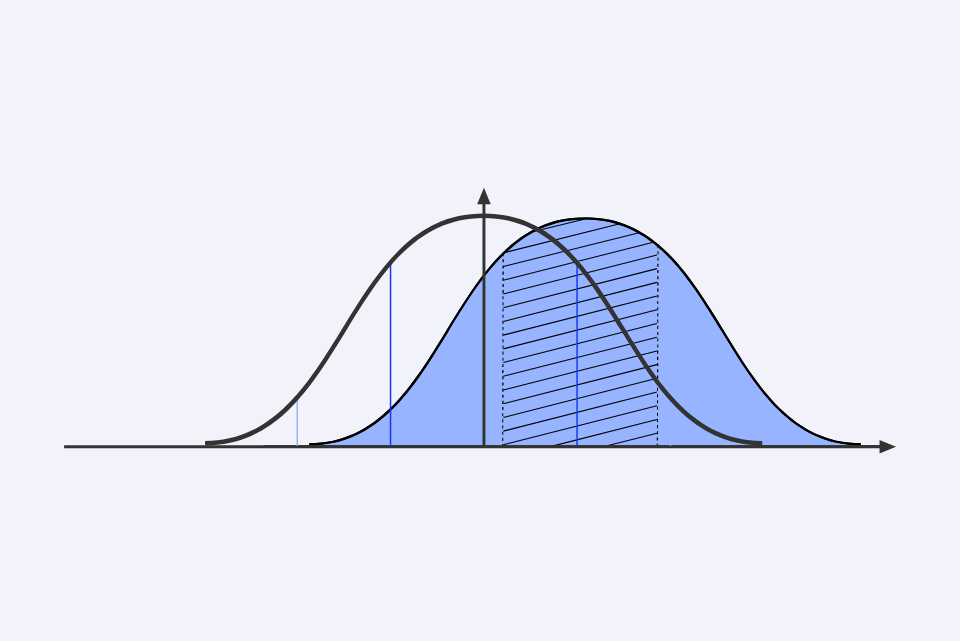
Die F-Distribution

Die F-Verteilung ist für die Bestimmung der statistischen Signifikanz Ihrer ANOVA-Ergebnisse unerlässlich. Es handelt sich um eine Wahrscheinlichkeitsverteilung, die häufig beim Umgang mit Varianzen auftritt.

• Die Form: Die F-Verteilung ist rechtsschief und variiert in Abhängigkeit von den Freiheitsgraden für den Zähler (zwischen den Gruppen) und den Nenner (innerhalb der Gruppen).
• Kritische Werte: Diese werden durch die F-Verteilung und das von Ihnen gewählte Signifikanzniveau (normalerweise 0,05) bestimmt. Wenn der von Ihnen berechnete F-Quotient den kritischen Wert überschreitet, lehnen Sie die Nullhypothese ab und kommen zu dem Schluss, dass signifikante Unterschiede zwischen den Gruppenmitteln bestehen.

Zur Verwendung der F-Verteilung ziehen Sie in der Regel F-Tabellen heran oder verwenden eine Statistiksoftware, die den p-Wert für Ihr F-Verhältnis angibt. Dieser p-Wert hilft bei der Entscheidung, ob die Nullhypothese angenommen oder abgelehnt werden soll.

Wenn Sie diese mathematischen Grundlagen verstehen, sind Sie in der Lage, die ANOVA effektiv einzusetzen und eine genaue und aussagekräftige statistische Analyse durchzuführen.

Arten von ANOVA

Die ANOVA gibt es in verschiedenen Formen, die jeweils für unterschiedliche Versuchspläne und Forschungsfragen geeignet sind. Wenn Sie diese Arten verstehen, können Sie die richtige Methode für Ihre Analyse auswählen.

Einfaktorielle ANOVA

Die einfaktorielle ANOVA ist die einfachste Form der ANOVA und wird verwendet, wenn die Mittelwerte von drei oder mehr unabhängigen Gruppen auf der Grundlage eines Faktors verglichen werden. Sie ist vorteilhaft, wenn es darum geht, festzustellen, ob es statistisch signifikante Unterschiede zwischen den Mittelwerten unabhängiger (unverbundener) Gruppen gibt.

Die einfaktorielle ANOVA wird verwendet, wenn es eine einzige unabhängige Variable mit mehreren Stufen und eine abhängige Variable gibt. Zum Beispiel könnten Sie die Testergebnisse von Schülern vergleichen, die mit drei verschiedenen Lehrmethoden unterrichtet wurden.

Mit unseremRechner für die einfaktorielle ANOVA können Sie diesen Test leicht durchführen.

Beispiel-Szenarien

Angenommen, Sie untersuchen die Wirkung verschiedener Düngemittel auf das Pflanzenwachstum. Sie haben drei Düngemitteltypen (A, B und C) und messen das Wachstum der Pflanzen mit jedem Typ.

Berechnung der einfaktoriellen ANOVA

1. Berechnen Sie die Gruppenmittelwerte: Berechnen Sie den Mittelwert für jeden Düngemitteltyp.
2. Gesamtmittelwert: Berechnen Sie den Mittelwert aller Datenpunkte zusammen.
   
   X_Gesamt = (ΣX_i) / n
3. Summe der Quadrate zwischen (SSB): Damit wird die Variation aufgrund der Interaktion zwischen den Gruppen gemessen.
   
   SSB = Σ (n_j * (X_j - X_gesamt)^2)
4. Summe der Quadrate innerhalb (SSW): Damit wird die Variation innerhalb jeder Gruppe gemessen.
   
   SSW = Σ Σ (X_ij - X_j)^2
5. Mittlere Quadrate: Berechnen Sie die mittleren Quadrate für zwischen den Gruppen (MSB) und innerhalb der Gruppen (MSW).
   
   MSB = SSB / dfB
   MSW = SSW / dfW
6. F-Verhältnis: Berechnen Sie den F-Quotienten, um festzustellen, ob die Varianz zwischen den Gruppenmitteln signifikant größer ist als die Varianz innerhalb der Gruppen.
   
   F = MSB / MSW

Zweifache ANOVA

Die zweifache ANOVA erweitert die einseitige ANOVA durch die Einbeziehung zweier unabhängiger Variablen. Mit dieser Methode können Sie die Wechselwirkung zwischen diesen Variablen und ihre individuellen Auswirkungen auf die abhängige Variable untersuchen.

Die zweifache ANOVA wird verwendet, wenn Sie zwei unabhängige Variablen haben. Sie könnten zum Beispiel die Auswirkungen verschiedener Diäten und Sportprogramme auf die Gewichtsabnahme untersuchen wollen.

Interaktionseffekte

Interaktionseffekte treten auf, wenn die Auswirkung einer unabhängigen Variable auf die abhängige Variable von der Höhe der anderen unabhängigen Variable abhängt. Das Verständnis dieser Interaktionen kann tiefere Einblicke in die Daten ermöglichen.

Zweifache ANOVA-Berechnung

1. Berechnen Sie die Gruppenmittelwerte: Berechnen Sie den Mittelwert für jede Kombination der Stufen der beiden Faktoren.
2. Summe der Quadrate: Berechnen Sie die Summe der Quadrate für jeden Haupteffekt und den Interaktionseffekt.
   
   SS_A = Σ n_ij * (X_A - X_Gesamt)^2
   SS_B = Σ n_ij * (X_B - X_Gesamt)^2
   SS_AB = Σ n_ij * (X_AB - X_gesamt)^2
3. Mittlere Quadrate: Berechnen Sie die mittleren Quadrate für jede Variationsquelle.
   
   MS_A = SS_A / dfA
   MS_B = SS_B / dfB
   MS_AB = SS_AB / dfAB
4. F-Verhältnisse: Berechnen Sie die F-Ratios für jeden Haupteffekt und den Interaktionseffekt.
   
   F_A = MS_A / MSW
   F_B = MS_B / MSW
   F_AB = MS_AB / MSW
5. Auswertung: Bestimmen Sie, ob die F-Ratios signifikant sind, um die Haupt- und Interaktionseffekte zu verstehen.

MANOVA (Multivariate ANOVA)

Die MANOVA erweitert die ANOVA durch die gleichzeitige Analyse mehrerer abhängiger Variablen. Diese Methode ist nützlich, wenn Sie die Wirkung unabhängiger Variablen auf mehrere Ergebnisse verstehen müssen.

MANOVA wird verwendet, wenn Sie mehr als eine abhängige Variable haben. Sie könnten zum Beispiel die Auswirkungen eines Schulungsprogramms auf die Leistung der Mitarbeiter und die Arbeitszufriedenheit untersuchen wollen.

Während bei der ANOVA jeweils nur eine abhängige Variable untersucht wird, werden bei der MANOVA mehrere abhängige Variablen bewertet, wobei ihre Korrelationen berücksichtigt werden und eine umfassendere Analyse möglich ist.

MANOVA-Berechnung

1. Berechnen Sie die Mittelwertvektoren: Berechnen Sie den Mittelwertvektor für jede Gruppe.
   
   X_Mittelwertvektor = (X1_Mittelwert, X2_Mittelwert, ..., Xk_Mittelwert)
2. Kovarianzmatrizen: Berechnen Sie die Kovarianzmatrizen innerhalb der Gruppe und zwischen den Gruppen.
   
   W = Σ (X_i - X_mean) * (X_i - X_mean)^T
   B = Σ n_j * (X_j - X_Gesamt)^2
3. Multivariate Teststatistiken: Um die multivariate Signifikanz zu bewerten, verwenden Sie Teststatistiken wie Wilks' Lambda, Pillai's Trace oder Hotelling's Trace.
   
   Wilks' Lambda = |W| / |W + B|
4. Signifikanztest: Vergleichen Sie die Teststatistiken mit kritischen Werten aus der multivariaten F-Verteilung, um die Signifikanz zu bestimmen.

Das Verständnis dieser ANOVA-Typen und ihrer Anwendungen hilft Ihnen, bessere Experimente zu planen und Daten effektiver zu analysieren, um tiefere Einblicke und genauere Schlussfolgerungen zu erhalten.

ANOVA-Annahmen und Vorbedingungen

Um die Gültigkeit Ihrer ANOVA-Ergebnisse zu gewährleisten, ist es wichtig, bestimmte Annahmen zu verstehen und zu erfüllen. Diese Annahmen bilden die Grundlage für die Genauigkeit und Zuverlässigkeit der Analyse.

Normalität

Normalität bezieht sich auf die Annahme, dass die Daten innerhalb jeder Gruppe einer Normalverteilung folgen. Diese Annahme ist von entscheidender Bedeutung, da sich die ANOVA auf den Mittelwert und die Varianz der Daten stützt, und die Normalität gewährleistet, dass diese Statistiken zuverlässig sind.

Wenn die Daten normalverteilt sind, sind die in der ANOVA verwendeten statistischen Tests genauer. Diese Annahme ist besonders wichtig bei kleineren Stichprobengrößen, bei denen Abweichungen von der Normalität die Ergebnisse erheblich beeinflussen können.

Testen auf Normalität

Mehrere Methoden können Ihnen helfen, die Normalität zu beurteilen:

• Q-Q-Diagramme: Diese Diagramme vergleichen die Quantile Ihrer Daten mit einer theoretischen Normalverteilung. Wenn die Datenpunkte ungefähr entlang einer geraden Linie liegen, sind die Daten wahrscheinlich normal.
• Shapiro-Wilk-Test: Dieser statistische Test prüft auf Normalität. Ein nicht-signifikantes Ergebnis (p > 0,05) deutet darauf hin, dass die Daten nicht signifikant von der Normalverteilung abweichen.
• Kolmogorov-Smirnov-Test: Ein weiterer Test auf Normalität, bei dem die Stichprobenverteilung mit einer Normalverteilung verglichen wird.

Wenn Ihre Daten von der Normalität abweichen, sollten Sie eine Transformation der Daten (z. B. Log-Transformation) oder nichtparametrische Alternativen wie den Kruskal-Wallis-Test in Betracht ziehen.

Homogenität der Varianzen

Homogenität der Varianzen oder Homoskedastizität bedeutet, dass die Varianzen innerhalb jeder Gruppe ungefähr gleich sind. Diese Annahme gewährleistet, dass der Vergleich der Mittelwerte zwischen den Gruppen fair und genau ist.

Wenn die Varianzen gleich sind, ist die gepoolte Schätzung der Varianz, die in ANOVA-Berechnungen verwendet wird, genau. Ungleiche Varianzen können zu verzerrten Ergebnissen und falschen Schlussfolgerungen führen.

Prüfung auf Homogenität

Mehrere Tests können die Homogenität der Varianzen überprüfen:

• Levene's Test: Mit diesem Test wird geprüft, ob die Varianzen zwischen den Gruppen gleich sind. Ein nicht-signifikantes Ergebnis (p > 0,05) deutet auf gleiche Varianzen hin.
• Bartlett's Test: Ein weiterer Test für gleiche Varianzen, der empfindlicher auf Abweichungen von der Normalität reagiert.
• Hartley's F-max Test: Dieser Test vergleicht die größten und kleinsten Varianzen zwischen den Gruppen.

Wenn die Varianzen ungleich sind, sollten Sie eine andere Version der ANOVA verwenden, z. B. die Welch'sche ANOVA, die robuster gegenüber Heteroskedastizität ist.

Unabhängigkeit der Beobachtungen

Unabhängigkeit bedeutet, dass die Beobachtungen innerhalb jeder Gruppe nicht miteinander verbunden sind. Mit dieser Annahme wird sichergestellt, dass die Varianz innerhalb der Gruppen echte individuelle Unterschiede und keine Muster oder Korrelationen widerspiegelt.

Sicherstellung der Unabhängigkeit

Die Unabhängigkeit wird in der Regel durch das Studiendesign sichergestellt:

• Randomisierung: Zuteilung der Probanden zu den Gruppen nach dem Zufallsprinzip, um Verzerrungen zu vermeiden.
• Verblindung: Verwenden Sie einfach oder doppelt verblindete Designs, um Verzerrungen zu reduzieren, die Beobachtungen korrelieren könnten.
• Angemessene Stichprobenverfahren: Stellen Sie sicher, dass die Stichproben unabhängig gezogen werden und die Grundgesamtheit genau repräsentieren.

Verstöße gegen die Unabhängigkeit können die ANOVA-Ergebnisse stark beeinträchtigen und sie unzuverlässig machen. Wenn die Beobachtungen nicht unabhängig sind, sollten Sie Techniken wie Modelle mit gemischten Effekten verwenden, die die fehlende Unabhängigkeit berücksichtigen.

Überprüfung der Annahmen mit Tests und Diagnosen

Bevor Sie eine ANOVA durchführen, müssen Sie unbedingt überprüfen, ob alle Annahmen erfüllt sind. Hier finden Sie einige praktische Schritte und Hilfsmittel:

Visuelle Diagnostik

• Box Plots: Diese Diagramme können Ihnen helfen, die Verteilung zu visualisieren und potenzielle Ausreißer zu identifizieren.
• Histogramme: Beurteilen Sie die Verteilung der Daten innerhalb jeder Gruppe.
• Streudiagramme: Suchen Sie nach Mustern, die auf eine Verletzung der Unabhängigkeit hindeuten könnten.

Statistische Tests

• Shapiro-Wilk-Test: Beurteilung der Normalität.
• Levene's Test: Überprüfung der Homogenität der Varianzen.
• Durbin-Watson-Statistik: Bewertung der Unabhängigkeit bei Zeitreihendaten.

Software-Tools

Statistische Softwarepakete (wie SPSS, R und Python-Bibliotheken) bieten integrierte Funktionen zur Durchführung dieser Tests und zur Erstellung von Diagnoseplots. Zum Beispiel:

• R: Funktionen wie shapiro.test(), leveneTest() und durbinWatsonTest() sind in verschiedenen Paketen verfügbar.
• SPSS: Bietet Point-and-Click-Optionen zur Durchführung dieser Tests.
• Python: Bibliotheken wie scipy.stats und statsmodels bieten Funktionen für diese Diagnosen.

Für die Gültigkeit der ANOVA-Ergebnisse ist es entscheidend, dass diese Annahmen erfüllt sind. Wenn Sie die Annahmen rigoros überprüfen, können Sie darauf vertrauen, dass Ihre Analyse sowohl genau als auch zuverlässig ist.

Wie führt man einen ANOVA-Test durch?

Die Durchführung einer ANOVA umfasst mehrere genau definierte Schritte, von der Planung Ihres Experiments bis zur Interpretation der Ergebnisse. Hier finden Sie einen detaillierten Leitfaden, der Ihnen hilft, diesen Prozess effektiv zu gestalten.

1. Entwurf eines Experiments

Ein gut durchdachtes Experiment ist die Grundlage für eine erfolgreiche ANOVA. Beginnen Sie damit, Ihre Forschungsfrage klar zu definieren und Ihre unabhängigen und abhängigen Variablen zu bestimmen. Bestimmen Sie die Anzahl der Stufen für Ihre unabhängige(n) Variable(n) und stellen Sie sicher, dass Sie über eine ausreichende Stichprobengröße verfügen, um aussagekräftige Unterschiede zu ermitteln.

Die Randomisierung ist entscheidend, um Verzerrungen auszuschließen und sicherzustellen, dass die Gruppen vergleichbar sind. Ziehen Sie in Erwägung, die Probanden nach dem Zufallsprinzip verschiedenen Behandlungsgruppen zuzuweisen. Wenn möglich, sollten Sie Methoden zur Verblindung einführen, um einen möglichen Einfluss von Erwartungen auf die Ergebnisse zu verringern.

2. Datenerhebung und Vorbereitung

Eine genaue Datenerfassung ist unerlässlich. Stellen Sie sicher, dass Ihre Messinstrumente zuverlässig und gültig sind. Erfassen Sie die Daten systematisch und einheitlich für alle Gruppen. Seien Sie bei der Aufzeichnung Ihrer Daten sorgfältig, um Fehler zu vermeiden.

Sobald die Datenerfassung abgeschlossen ist, bereiten Sie Ihre Daten für die Analyse vor. Dazu gehört die Überprüfung auf fehlende Werte, Ausreißer und Fehler. Bereinigen Sie Ihre Daten, um sicherzustellen, dass sie für die ANOVA geeignet sind. Die richtige Kodierung Ihrer Variablen ist ebenfalls wichtig. Wenn Sie zum Beispiel kategorischen Variablen numerische Werte zuweisen, kann dies den Analyseprozess vereinfachen.

3. Durchführen der ANOVA mit statistischer Software

Mehrere Statistiksoftwarepakete, darunter SPSS, R und Python, können ANOVA durchführen. Im Folgenden finden Sie einen kurzen Überblick über die Durchführung von ANOVA mit diesen Tools:

SPSS

1. Daten eingeben: Geben Sie Ihre Daten in den SPSS-Dateneditor ein.
2. Definieren Sie Variablen: Gehen Sie zur Variablenansicht und definieren Sie Ihre unabhängigen und abhängigen Variablen.
3. ANOVA ausführen: Navigieren Sie zu Analysieren > Mittelwerte vergleichen > Einseitige ANOVA für eine einseitige ANOVA oder Analysieren > Allgemeines lineares Modell > Univariate für komplexere Designs.
4. Optionen festlegen: Wählen Sie bei Bedarf die entsprechenden Optionen für Post-hoc-Tests und Effektgröße.
5. Ausgabe interpretieren: Überprüfen Sie die ANOVA-Tabelle auf den F-Wert und den p-Wert, um die Signifikanz zu bestimmen.

R

1. Daten laden: Importieren Sie Ihren Datensatz mit Funktionen wie read.csv() oder read.table().
2. ANOVA-Modell anpassen: Verwenden Sie die Funktion aov() für eine einseitige ANOVA oder anova() für komplexere Designs. Beispiel: model <- aov(abhängige_Variable ~ unabhängige_Variable, data = dataset).
3. Zusammenfassung: Generieren Sie eine Zusammenfassung des Modells mit summary(model).
4. Post-Hoc-Tests: Führen Sie Post-Hoc-Tests mit Funktionen wie TukeyHSD(model) durch.

Python

1. Bibliotheken laden: Importieren Sie notwendige Bibliotheken wie pandas, scipy.stats und statsmodels.
2. Daten laden: Verwenden Sie pandas, um Ihre Daten zu lesen, z. B. data = pd.read_csv('yourfile.csv').
3. ANOVA-Modell anpassen: Verwenden Sie stats.f_oneway() für eine einseitige ANOVA oder ols() von statsmodels für komplexere Designs.
4. Ergebnisse interpretieren: Untersuchen Sie die Ausgabe auf F-Werte und p-Werte.

Mit Appinio können Sie den gesamten Prozess der ANOVA-Durchführung rationalisieren, ohne dass Sie komplexe Methoden oder Software benötigen. Entwerfen Sie Experimente, sammeln Sie zuverlässige Daten und führen Sie detaillierte ANOVA-Analysen durch - alles auf einer einzigen Plattform. Das bedeutet, dass Sie sich mehr auf die Interpretation Ihrer Ergebnisse und datengestützte Entscheidungen konzentrieren können, anstatt sich mit technischen Details aufzuhalten.

Entdecken Sie, wie einfach und effizient es sein kann, verwertbare Erkenntnisse zu gewinnen und Ihre Forschung voranzutreiben!

4. Ergebnisse interpretieren

Nach der Durchführung einer ANOVA ist die richtige Interpretation der Ergebnisse entscheidend:

• F-Statistik: Dieser Wert gibt das Verhältnis der Varianz zwischen den Gruppen zur Varianz innerhalb der Gruppen an. Ein höherer F-Wert deutet auf einen signifikanteren Unterschied zwischen den Gruppen hin.
• P-Wert: Dieser Wert hilft bei der Bestimmung der statistischen Signifikanz. Ein p-Wert von weniger als 0,05 weist in der Regel auf signifikante Unterschiede zwischen den Gruppen hin.
• Post-Hoc-Tests: Wenn Ihre ANOVA-Ergebnisse signifikant sind, können Post-Hoc-Tests (wie Tukey's HSD) ermitteln, welche Gruppen sich voneinander unterscheiden.
• Effektgröße: Ziehen Sie die Berechnung der Effektgröße in Betracht, um das Ausmaß der Unterschiede und nicht nur ihre Signifikanz zu verstehen. Zu den Standardmaßen gehören Eta-Quadrat und Cohen's d.

5. Berichterstattung über die Ergebnisse

Es ist wichtig, dass Sie Ihre ANOVA-Ergebnisse klar und präzise darstellen. Fügen Sie Folgendes in Ihren Bericht ein:

• Deskriptive Statistik: Mittelwert und Standardabweichung für jede Gruppe.
• ANOVA-Tabelle: F-Wert, Freiheitsgrade und p-Wert.
• Post-Hoc-Testergebnisse: Detaillierte Ergebnisse aller Post-Hoc-Analysen.
• Auswertung: Eine klare Interpretation der Ergebnisse, einschließlich praktischer oder theoretischer Implikationen.

Wenn Sie diese Schritte befolgen, können Sie eine ANOVA sicher durchführen und sicherstellen, dass Ihre Ergebnisse genau und aussagekräftig sind. Unabhängig davon, ob Sie SPSS, R oder Python verwenden, bleiben die Grundsätze dieselben: ein solides Design, eine sorgfältige Datenaufbereitung sowie eine gründliche Analyse und Interpretation.

ANOVA vs. andere statistische Tests

Die Wahl eines geeigneten statistischen Tests ist entscheidend für eine genaue Analyse und aussagekräftige Ergebnisse. Die ANOVA ist ein leistungsfähiges Werkzeug, aber wenn Sie verstehen, wie sie im Vergleich zu anderen statistischen Tests abschneidet, können Sie die beste Wahl für Ihre Daten treffen.

ANOVA vs. T-Test

Der t-Test ist ein weiterer weit verbreiteter statistischer Test, der hauptsächlich für den Vergleich der Mittelwerte zweier Gruppen verwendet wird. Hier erfahren Sie, wie sich ANOVA und t-Test unterscheiden und wann Sie beide verwenden sollten:

Anzahl der Gruppen

• T-Test: Ideal für den Vergleich der Mittelwerte von zwei Gruppen. Es gibt zwei Arten von t-Tests: unabhängige (für zwei getrennte Gruppen) und gepaarte (für zwei verwandte Gruppen).
• ANOVA: Entwickelt für den Vergleich der Mittelwerte von drei oder mehr Gruppen. Sie kann mit komplexeren Versuchsplänen mit mehreren Gruppen und Faktoren umgehen.

Beispiel

Betrachten wir eine Studie, in der die Auswirkungen von zwei Diäten auf die Gewichtsabnahme verglichen werden. Hier ist ein t-Test geeignet, da es nur zwei Gruppen gibt. Wenn Sie jedoch eine dritte Diät einführen, ist die ANOVA die richtige Wahl.

Annahmen

Für beide Tests gelten ähnliche Annahmen, darunter Normalität, Homogenität der Varianzen und Unabhängigkeit. Wenn diese Annahmen nicht erfüllt sind, sollten Sie nicht-parametrische Alternativen wie den Mann-Whitney-U-Test für den t-Test und den Kruskal-Wallis-Test für die ANOVA verwenden.

t-Test-Rechner:

ANOVA vs. Regressionsanalyse

Bei der Regressionsanalyse wird die Beziehung zwischen abhängigen und unabhängigen Variablen untersucht. Sie ist vielseitig und kann mit verschiedenen Arten von Daten und Beziehungen umgehen. Hier ist ein Vergleich:

Schwerpunkt

• ANOVA: Konzentriert sich in erster Linie auf den Vergleich von Mittelwerten zwischen verschiedenen Gruppen und die Feststellung, ob diese Mittelwerte signifikant unterschiedlich sind.
• Regression: Untersucht die Beziehung zwischen abhängigen und unabhängigen Variablen und sagt die abhängige Variable auf der Grundlage eines oder mehrerer Prädiktoren voraus.

Komplexität

• ANOVA: Einfacher zu verwenden für einfache Vergleiche und Versuchspläne mit kategorialen unabhängigen Variablen.
• Regression: Ist flexibler und kann sowohl kategoriale als auch kontinuierliche Variablen, Interaktionseffekte und polynomiale Terme zur Modellierung komplexer Beziehungen einbeziehen.

Beispiel

Angenommen, Sie untersuchen die Auswirkungen von Bildungsniveau und Berufserfahrung auf das Gehalt. Mit der Regressionsanalyse können Sie beide Faktoren und ihre Interaktion einbeziehen und so ein detailliertes Modell ihres Einflusses auf das Gehalt erstellen.

ANOVA vs. Chi-Quadrat-Test

Der Chi-Quadrat-Test wird für kategoriale Daten verwendet, um den Zusammenhang zwischen Variablen zu bewerten. Hier ist der Vergleich mit der ANOVA:

Datentyp

• ANOVA: Wird für kontinuierliche Daten verwendet, bei denen Sie an einem Vergleich der Gruppenmittelwerte interessiert sind.
• Chi-Quadrat-Test: Geeignet für kategoriale Daten, bei denen Sie die Beziehung oder Unabhängigkeit zwischen kategorialen Variablen untersuchen.

Beispiel

Wenn Sie die Durchschnittsnoten von Schülern verschiedener Schulen vergleichen möchten, ist die ANOVA geeignet. Wenn Sie jedoch daran interessiert sind, ob sich die Verteilung der bevorzugten Lernmethoden der Schüler (z. B. online, persönlich, hybrid) nach Schule unterscheidet, ist der Chi-Quadrat-Test die richtige Wahl.

Annahmen

• ANOVA: Setzt Normalität, Homogenität der Varianzen und Unabhängigkeit voraus.
• Chi-Quadrat-Test: Setzt eine ausreichend große Stichprobe voraus und dass die Daten kategorisch sind.

Chi-Quadrat-Rechner:

ANOVA vs. MANOVA

MANOVA (Multivariate ANOVA) ist eine Erweiterung der ANOVA, die mit mehreren abhängigen Variablen arbeitet. Hier ist der Unterschied:

Anzahl der abhängigen Variablen

• ANOVA: Wird verwendet, wenn es nur eine abhängige Variable gibt.
• MANOVA: Geeignet für die gleichzeitige Analyse mehrerer abhängiger Variablen unter Berücksichtigung der Korrelation zwischen ihnen.

Beispiel

Wenn Sie die Auswirkung eines Schulungsprogramms auf die Leistung Ihrer Mitarbeiter bewerten wollen, eignet sich die ANOVA für eine einzige Leistungskennzahl. Wenn Sie jedoch Leistung, Arbeitszufriedenheit und Mitarbeiterbindung gleichzeitig bewerten möchten, bietet MANOVA eine umfassendere Analyse.

Praktische Überlegungen

Bei der Entscheidung zwischen diesen Tests sollten Sie Folgendes berücksichtigen:

• Forschungsfrage: Definieren Sie klar, was Sie herausfinden wollen. Vergleichen Sie Mittelwerte, erkunden Sie Beziehungen oder untersuchen Sie Assoziationen?
• Datentyp: Stellen Sie sicher, dass Ihre Daten den Anforderungen des Tests entsprechen (kontinuierlich oder kategorisch).
• Annahmen: Prüfen Sie, ob Ihre Daten die Annahmen des Testserfüllen. Falls nicht, suchen Sie nach robusten oder nicht-parametrischen Alternativen.
• Kompliziertheit: Wählen Sie einen Test, der Ihren statistischen Kenntnissen und der Komplexität Ihrer Daten entspricht.

Wenn Sie die Unterschiede zwischen ANOVA und anderen statistischen Tests kennen, können Sie die für Ihre Analyse am besten geeignete Methode wählen. Dies gewährleistet genaue, zuverlässige und aussagekräftige Ergebnisse, die letztlich zu fundierteren Entscheidungen und Erkenntnissen führen.

Schlussfolgerung für ANOVA

Die ANOVA ist ein unverzichtbares Werkzeug im Werkzeugkasten des Statistikers, das eine robuste Methode für den Vergleich mehrerer Gruppen und das Verständnis der Variabilität innerhalb von Daten bietet. Durch die Aufteilung der Varianz in aussagekräftige Komponenten hilft die ANOVA bei der Feststellung, ob die beobachteten Unterschiede in den Gruppenmitteln statistisch signifikant oder lediglich das Ergebnis eines Zufalls sind. In diesem Leitfaden wurden die grundlegenden Konzepte, die mathematischen Grundlagen, die verschiedenen Arten der ANOVA und die Bedeutung der Einhaltung von Annahmen für genaue Ergebnisse untersucht. Unabhängig davon, ob Sie eine einseitige, zweiseitige oder multivariate ANOVA verwenden, bleiben die Grundsätze dieselben: ein rigoroser Ansatz zur Analyse von Daten und zum Ziehen zuverlässiger Schlussfolgerungen.

Das Verständnis für die Anwendung der ANOVA in realen Szenarien, von klinischen Studien bis hin zur Marktforschung, unterstreicht ihre Vielseitigkeit und Bedeutung. Die Beherrschung der ANOVA ermöglicht es Ihnen, bessere Experimente zu planen, fundiertere Entscheidungen zu treffen und wertvolle Erkenntnisse zu Ihrem Fachgebiet beizutragen. Dieser Leitfaden soll die ANOVA entmystifizieren und Sie mit dem Wissen und den Werkzeugen ausstatten, die Sie zur sicheren Anwendung dieser Technik benötigen. Denken Sie bei Ihrer weiteren Arbeit mit Daten daran, dass die ANOVA nicht nur ein statistischer Test ist, sondern ein Tor zu tieferen Einsichten und effektiveren Strategien auf der Grundlage empirischer Erkenntnisse.

Wie führt man einen ANOVA-Test in wenigen Minuten durch?

Appinio revolutioniert die Art und Weise, wie Unternehmen ANOVA durchführen, indem es eine Echtzeit-Marktforschungsplattform anbietet, die das Sammeln von Kundeneinblicken schnell, intuitiv und spannend macht. Mit Appinio können Unternehmen mühelos ANOVA durchführen, um mehrere Gruppen zu vergleichen und verwertbare Erkenntnisse zu gewinnen, ohne sich mit langwierigen, komplizierten und teuren Forschungsprozessen herumschlagen zu müssen.

Die benutzerfreundliche Oberfläche der Plattform und die schnelle Datenerfassung sorgen dafür, dass jeder, unabhängig von seinem Forschungshintergrund, anspruchsvolle statistische Analysen wie ANOVA durchführen und datengestützte Entscheidungen in wenigen Minuten treffen kann.

• Schnelle Einblicke: Von der Formulierung der Fragen bis zur Gewinnung umfassender Erkenntnisse liefert Appinio in weniger als 23 Minuten Ergebnisse für bis zu 1.000 Befragte und stellt damit sicher, dass Sie schnell über die Daten verfügen, die Sie für zeitnahe Geschäftsentscheidungen benötigen.
• Intuitive Plattform: Die auf Benutzerfreundlichkeit ausgelegte Plattform von Appinio ermöglicht es jedem, gründliche Marktforschung und ANOVA durchzuführen, ohne dass er über fortgeschrittenes Forschungswissen oder einen Doktortitel verfügen muss. Die intuitive Benutzeroberfläche führt die Nutzer nahtlos durch den Prozess.
• Globale Reichweite und Präzision: Mit der Möglichkeit, Zielgruppen aus über 1.200 Merkmalen und Umfrageteilnehmern in mehr als 90 Ländern zu definieren, stellt Appinio sicher, dass Ihre Forschung sowohl präzise als auch global repräsentativ ist und die Breite und Tiefe der Erkenntnisse liefert, die für strategische Entscheidungen erforderlich sind.

Kostenlos registrieren

Kostenlosen Zugang zur Appinio Platform erhalten!

Or

Continue with Google Continue with Microsoft