Was ist ein Konfidenzintervall und wie kann es berechnet werden?

Haben Sie sich schon einmal gefragt, wie wir auf der Grundlage von Stichprobendaten Bevölkerungsparameter wie die Durchschnittsgröße der Menschen in einer Stadt oder den Anteil der Wähler, die einen bestimmten Kandidaten unterstützen, genau schätzen können? An dieser Stelle kommen Konfidenzintervalle ins Spiel. Konfidenzintervalle liefern uns einen Bereich plausibler Werte für Bevölkerungsparameter sowie ein Maß dafür, wie sicher wir uns auf diese Schätzungen verlassen können. Sie helfen uns dabei, die mit statistischen Analysen verbundene Unsicherheit zu quantifizieren und fundierte Entscheidungen in verschiedenen Bereichen zu treffen, von der wissenschaftlichen Forschung bis hin zu Wirtschaft und Politik.

In diesem Leitfaden befassen wir uns mit Konfidenzintervallen, ihrer Bedeutung, Berechnungsmethoden, fortgeschrittenen Techniken und vielem mehr. Egal, ob Sie studieren, forschen oder beruflich tätig sind und statistische Konzepte verstehen und anwenden möchten, dieses Handbuch wird Ihnen das Wissen und die Werkzeuge an die Hand geben, die Sie benötigen, um Populationsparameter mit Präzision und Genauigkeit zu schätzen und zu interpretieren.

Was ist ein Konfidenzintervall?

Ein Konfidenzintervall ist ein statistisches Hilfsmittel zur Schätzung des Wertebereichs, in dem ein Populationsparameter, wie z. B. ein Populationsmittelwert oder -anteil, wahrscheinlich liegt. Es stellt ein Maß für die Unsicherheit um eine aus Stichprobendaten abgeleitete Punktschätzung dar.

Konfidenzintervalle werden auf der Grundlage von Stichprobenstatistiken, wie z. B. dem Stichprobenmittelwert oder -anteil, konstruiert und sind in der Regel mit einem bestimmten Konfidenzniveau, wie z. B. 95 % oder 99 %, versehen. Das Konfidenzniveau gibt die Wahrscheinlichkeit an, dass das berechnete Intervall bei wiederholten Stichproben den wahren Populationsparameter enthält.

Die Bedeutung von Konfidenzintervallen in der statistischen Analyse

• Quantifizierung der Ungewissheit: Konfidenzintervalle sind ein Maß für die Unsicherheit von Punktschätzungen und ermöglichen es Forschern, die Zuverlässigkeit und Genauigkeit ihrer Ergebnisse zu bewerten. Konfidenzintervalle helfen, übermäßiges Vertrauen in statistische Schätzungen zu vermeiden, indem sie die Unsicherheit anerkennen und quantifizieren.
• Inferenz und Entscheidungsfindung: Konfidenzintervalle spielen eine entscheidende Rolle bei statistischen Schlussfolgerungen und bei der Entscheidungsfindung. Sie ermöglichen es Forschern, auf der Grundlage von Stichprobendaten Rückschlüsse auf Populationsparameter zu ziehen und so Entscheidungen in Forschung, Wirtschaft, Gesundheitswesen und Politik zu treffen.
• Vergleich von Gruppen oder Behandlungen: Konfidenzintervalle erleichtern Vergleiche zwischen Gruppen oder Behandlungen, indem sie einen Bereich von plausiblen Werten für Populationsparameter angeben. Unabhängig davon, ob Mittelwerte, Proportionen oder andere Statistiken verglichen werden, helfen Konfidenzintervalle bei der Bewertung der Signifikanz und des Ausmaßes von Unterschieden.
• Bestimmung des Stichprobenumfangs: Konfidenzintervalle dienen der Bestimmung des Stichprobenumfangs für Forschungsstudien. Durch die Angabe des gewünschten Präzisions- und Konfidenzniveaus können Forscher den Stichprobenumfang berechnen, der zum Erreichen ihrer Studienziele erforderlich ist, während gleichzeitig Kosten und Ressourcen minimiert werden.
• Kommunikation der Ergebnisse: Konfidenzintervalle bieten eine prägnante Möglichkeit, die Präzision und Unsicherheit statistischer Schätzungen den Beteiligten, einschließlich Forschern, politischen Entscheidungsträgern und der breiten Öffentlichkeit, zu vermitteln. Sie geben einen klaren Hinweis auf den Bereich, in den der wahre Populationsparameter wahrscheinlich fällt.
• Robustheit gegenüber Annahmen: Im Gegensatz zu Punktschätzungen, die empfindlich auf Ausreißer oder Verletzungen der Verteilungsannahmen reagieren können, sind Konfidenzintervalle robuster und vermitteln ein umfassenderes Bild der zugrunde liegenden Unsicherheit. Sie bieten einen flexiblen Ansatz für die statistische Analyse, insbesondere in Situationen, in denen parametrische Annahmen möglicherweise nicht zutreffen.
• Qualitätskontrolle und Prozessverbesserung: Bei der Qualitätskontrolle und Prozessverbesserung werden Konfidenzintervalle zur Überwachung und Bewertung der Leistung von Systemen und Prozessen verwendet. Durch die Verfolgung von Konfidenzintervallen im Zeitverlauf können Unternehmen Trends erkennen, Abweichungen von der erwarteten Leistung feststellen und bei Bedarf Korrekturmaßnahmen einleiten.
• Wissenschaftliche Reproduzierbarkeit: Konfidenzintervalle tragen zur Transparenz und Reproduzierbarkeit wissenschaftlicher Forschung bei, indem sie die mit statistischen Schätzungen verbundene Unsicherheit quantifizieren. In Replikationsstudien können Konfidenzintervalle verwendet werden, um die Konsistenz und Verallgemeinerbarkeit von Ergebnissen über verschiedene Stichproben oder Umgebungen hinweg zu bewerten.
• Entscheidungsfindung unter Unsicherheit: In Entscheidungskontexten bieten Konfidenzintervalle den Entscheidungsträgern einen Rahmen für die Berücksichtigung von Unsicherheit und Variabilität bei ihren Entscheidungen. Ob bei der Bewertung der Wirksamkeit von Maßnahmen, der Risikobewertung oder der Zuweisung von Ressourcen - Konfidenzintervalle liefern fundiertere und solidere Entscheidungen.

Verstehen von Konfidenzintervallen

Konfidenzintervalle sind ein Eckpfeiler der statistischen Inferenz und ermöglichen es uns, Populationsparameter mit einem gewissen Grad an Unsicherheit zu schätzen. Im Kern ist ein Konfidenzintervall ein aus Stichprobendaten abgeleiteter Wertebereich, der wahrscheinlich den wahren Populationsparameter enthält.

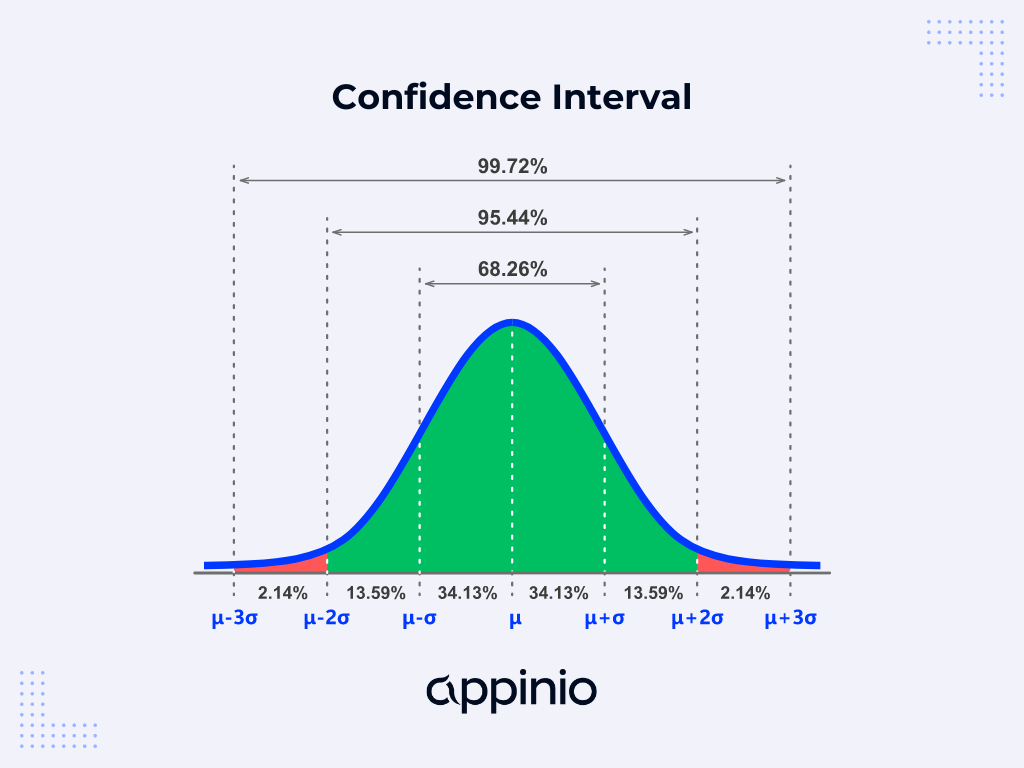
Stellen Sie sich vor, Sie versuchen, die durchschnittliche Körpergröße aller Erwachsenen in einem Land zu schätzen. Anstatt sich nur auf den Mittelwert der Stichprobe zu verlassen, der von Stichprobe zu Stichprobe variieren kann, liefert ein Konfidenzintervall einen Bereich plausibler Werte, in den der wahre Mittelwert der Bevölkerung voraussichtlich fallen wird. Dieser Bereich wird mit einem bestimmten Konfidenzniveau angegeben, in der Regel 95 % oder 99 %.

Interpretation des Konfidenzintervalls

Zur Interpretation eines Konfidenzintervalls gehört, dass man versteht, was das Intervall darstellt und was es nicht darstellt. Es ist wichtig zu verstehen, dass sich das mit einem Intervall verbundene Konfidenzniveau auf den Prozentsatz der aus wiederholten Stichproben abgeleiteten Konfidenzintervalle bezieht, die den wahren Populationsparameter enthalten würden. Wenn wir beispielsweise 100 Konfidenzintervalle mit einem Konfidenzniveau von 95 % konstruieren, würden wir erwarten, dass etwa 95 von ihnen den wahren Populationsparameter enthalten.

Bei der Übermittlung der Ergebnisse eines Konfidenzintervalls ist es wichtig zu betonen, dass es einen Bereich plausibler Werte und keine spezifische Punktschätzung liefert. Außerdem quantifiziert das Konfidenzintervall nur die Unsicherheit aufgrund der Stichprobenvariabilität und berücksichtigt keine anderen Quellen der Unsicherheit oder Verzerrung.

Wie berechnet man das Konfidenzintervall?

Die Berechnung eines Konfidenzintervalls hängt von mehreren Faktoren ab, darunter dem Stichprobenumfang, der Variabilität der Grundgesamtheit und dem gewünschten Konfidenzniveau. Für normalverteilte Daten mit einer bekannten Standardabweichung der Grundgesamtheit lautet die Formel zur Berechnung eines Konfidenzintervalls für den Grundgesamtheitsmittelwert (μ):

CI = x̄ ± Z(σ/√n)

Wobei:

• x̄ ist der Stichprobenmittelwert.
• σ ist die Standardabweichung der Grundgesamtheit.
• n ist der Stichprobenumfang.
• Z ist der kritische Wert aus der Standardnormalverteilung, der dem gewünschten Konfidenzniveau entspricht.

In Fällen, in denen die Standardabweichung der Grundgesamtheit nicht bekannt ist oder der Stichprobenumfang gering ist, wird die t-Verteilung anstelle der Standardnormalverteilung verwendet. Diese Anpassung trägt der zusätzlichen Unsicherheit Rechnung, die durch die Schätzung der Standardabweichung der Grundgesamtheit anhand der Stichprobendaten entsteht.

Die Automatisierung Ihrer Datenerfassungs- und Analyseprozesse mit Appinio macht manuelle Berechnungen überflüssig und rationalisiert Ihren Arbeitsablauf. Mithilfe unserer Plattform können Sie mühelos Konfidenzintervalle generieren, Zeit sparen und die Genauigkeit Ihrer statistischen Analysen sicherstellen. Verabschieden Sie sich von mühsamen Zahlenberechnungen und freuen Sie sich auf verwertbare Erkenntnisse, die Sie auf Knopfdruck erhalten.

 

Sind Sie bereit, Ihren Forschungsansatz zu revolutionieren? Buchen Sie noch heute eine Demo und entdecken Sie die Leistungsfähigkeit von Appinio aus erster Hand!

Demo buchen

Jetzt mit unseren Experten sprechen!

Wie findet man Konfidenzintervalle?

Konfidenzintervalle werden von verschiedenen Faktoren beeinflusst, die sich auf ihre Breite und Genauigkeit auswirken. Das Verständnis dieser Faktoren ist für die genaue Interpretation und Erstellung von Konfidenzintervallen unerlässlich.

Stichprobengröße

Der Stichprobenumfang spielt eine entscheidende Rolle bei der Bestimmung der Genauigkeit eines Konfidenzintervalls. Ein größerer Stichprobenumfang führt in der Regel zu engeren Intervallen und einer höheren Präzision bei der Schätzung von Populationsparametern. Dies liegt daran, dass größere Stichproben mehr Informationen über die Grundgesamtheit liefern, was zu zuverlässigeren Schätzungen führt.

Bei einem geringen Stichprobenumfang sind die Konfidenzintervalle tendenziell breiter, was die größere Unsicherheit widerspiegelt, die mit der Schätzung von Populationsparametern aus begrenzten Daten verbunden ist. Der Standardfehler sinkt mit zunehmendem Stichprobenumfang, was zu engeren Intervallen führt.

Nehmen wir zum Beispiel die Schätzung des Durchschnittseinkommens der Haushalte in einer Stadt. Ein größerer Stichprobenumfang würde eine repräsentativere Stichprobe der Bevölkerung ergeben, was zu einem engeren Konfidenzintervall und einer genaueren Schätzung des mittleren Einkommens der Bevölkerung führt.

Die Stichprobengröße ist ein entscheidender Faktor bei der Bestimmung der Genauigkeit von Konfidenzintervallen. Mit dem Stichprobengrößenrechner von Appinio können Sie sicherstellen, dass Ihre Umfrageergebnisse wirklich repräsentativ für die untersuchte Population sind. Durch Eingabe der gewünschten Fehlerspanne, des Konfidenzniveaus und der Standardabweichung berechnet der Rechner die für zuverlässige Ergebnisse erforderliche Mindeststichprobengröße.

Mit diesem leistungsstarken Tool können Sie Umfragen durchführen und sicher sein, dass Ihre Daten die breite Bevölkerung genau widerspiegeln. 

Konfidenzniveau

Das Konfidenzniveau bestimmt die Wahrscheinlichkeit, dass das Konfidenzintervall bei wiederholten Stichproben den wahren Populationsparameter enthält. Üblicherweise werden Konfidenzniveaus von 95 % und 99 % verwendet, doch können je nach gewünschter Sicherheit auch andere Niveaus gewählt werden.

Ein höheres Konfidenzniveau entspricht einem breiteren Konfidenzintervall, da es ein höheres Maß an Gewissheit erfordert, dass das Intervall den wahren Parameter enthält. Beispielsweise ergibt ein Konfidenzniveau von 99 % ein breiteres Intervall als ein Konfidenzniveau von 95 %, da es einen größeren Wertebereich umfasst, um der erhöhten Sicherheit Rechnung zu tragen.

Bei der Wahl des geeigneten Konfidenzniveaus gilt es, ein Gleichgewicht zwischen dem Bedarf an Präzision und dem gewünschten Konfidenzniveau der Schätzung herzustellen. Ein höheres Konfidenzniveau bietet zwar mehr Sicherheit, geht aber mit breiteren Intervallen und einer potenziell geringeren Präzision bei der Schätzung des Populationsparameters einher.

Variabilität der Bevölkerung

Die Populationsvariabilität bezieht sich auf das Ausmaß, in dem einzelne Beobachtungen in der Population vom Populationsmittelwert abweichen. Eine höhere Variabilität in der Grundgesamtheit führt zu breiteren Konfidenzintervallen, da die Unsicherheit bei der Schätzung des Populationsparameters anhand der Stichprobe größer ist.

Wenn die Variabilität der Grundgesamtheit hoch ist, streuen die einzelnen Beobachtungen stärker um den Mittelwert der Grundgesamtheit, wodurch es schwieriger wird, den wahren Parameter anhand einer Stichprobe genau zu schätzen. Infolgedessen müssen die Konfidenzintervalle breiter sein, um dieser größeren Unsicherheit Rechnung zu tragen.

Nehmen wir zum Beispiel die Schätzung der durchschnittlichen Testergebnisse von Schülern in zwei Schulen. Wenn eine Schule im Vergleich zur anderen ein breiteres Spektrum an Testergebnissen aufweist, wäre das Konfidenzintervall für das durchschnittliche Testergebnis in dieser Schule aufgrund der höheren Variabilität der Population breiter.

Durch die Berücksichtigung des Einflusses von Faktoren wie Stichprobengröße, Konfidenzniveau und Populationsvariabilität können Forscher Konfidenzintervalle konstruieren, die die mit der Schätzung von Populationsparametern aus Stichprobendaten verbundene Unsicherheit genau widerspiegeln. Dieses Verständnis ermöglicht eine fundierte Entscheidungsfindung und robuste statistische Schlussfolgerungen.

Arten von Konfidenzintervallen

Konfidenzintervalle können auf die Schätzung verschiedener Populationsparameter zugeschnitten werden, die jeweils unterschiedliche analytische Anforderungen erfüllen. Sehen wir uns die verschiedenen Arten von Konfidenzintervallen an und wie sie bei statistischen Schlussfolgerungen eingesetzt werden.

Konfidenzintervall für den Mittelwert der Grundgesamtheit

Das Konfidenzintervall für den Populationsmittelwert ist vielleicht die am häufigsten verwendete Art von Konfidenzintervall. Es liefert eine Schätzung, wo der wahre Mittelwert der Population mit einem bestimmten Vertrauensniveau liegt.

Formel für das Konfidenzintervall für den Mittelwert der Grundgesamtheit

Die Formel zur Berechnung des Konfidenzintervalls für den Mittelwert der Grundgesamtheit (μ) lautet:

CI = x̄ ± Z(σ/√n)

Wobei:

• x̄ ist der Stichprobenmittelwert.
• σ ist die Standardabweichung der Grundgesamtheit.
• n ist der Stichprobenumfang.
• Z ist der kritische Wert aus der Standardnormalverteilung, der dem gewünschten Konfidenzniveau entspricht.

Beispiel:

Angenommen, wir wollen die durchschnittliche Verweildauer der Kunden in einem Geschäft schätzen. Wir erheben eine Stichprobe von 100 Kunden und stellen fest, dass die durchschnittliche Verweildauer 30 Minuten beträgt, mit einer Standardabweichung von 5 Minuten. Wenn wir ein 95 %-Konfidenzintervall für den Mittelwert der Verweildauer in der Grundgesamtheit konstruieren wollen, können wir die folgende Formel verwenden:

CI = 30 ± 1,96(5/√100)

CI = 30 ± 0,98

Das 95 %ige Konfidenzintervall für die durchschnittliche Verweildauer der Kunden in der Filiale liegt also zwischen 29,02 und 30,98 Minuten.

Konfidenzintervall für den Anteil an der Bevölkerung

Bei kategorialen Daten, wie dem Anteil von Personen mit einem bestimmten Merkmal in einer Population, wird das Konfidenzintervall für den Populationsanteil verwendet.

Formel für das Konfidenzintervall für den Bevölkerungsanteil

Die Formel zur Berechnung des Konfidenzintervalls für den Bevölkerungsanteil (p) lautet:

CI = p̂ ± Z√[(p̂(1-p̂))/n]

Wobei:

• p̂ ist der Stichprobenanteil.
• n ist der Stichprobenumfang.
• Z ist der kritische Wert aus der Standardnormalverteilung, der dem gewünschten Konfidenzniveau entspricht.

Beispiel:

Angenommen, wir führen eine Umfrage durch, um den Anteil der Erwachsenen in einer Stadt zu schätzen, die ein Smartphone besitzen. Von einer Stichprobe von 500 befragten Erwachsenen besitzen 320 ein Smartphone. Um ein 90 %-Konfidenzintervall für den Bevölkerungsanteil der Erwachsenen, die ein Smartphone besitzen, zu erstellen, können wir die Formel verwenden:

CI = 0,64 ± 1,645√[(0,64(1-0,64))/500]

CI = 0,64 ± 0,036

Das 90%ige Konfidenzintervall für den Bevölkerungsanteil der Erwachsenen, die ein Smartphone besitzen, liegt also bei 0,604 bis 0,676.

Konfidenzintervall für die Differenz zwischen den Mittelwerten

Beim Vergleich zweier Populationen oder Gruppen, z. B. der Wirksamkeit zweier Behandlungen, wird das Konfidenzintervall für die Differenz zwischen den Mittelwerten verwendet.

Formel für das Konfidenzintervall für die Differenz zwischen den Mittelwerten

Die Formel zur Berechnung des Konfidenzintervalls für die Differenz zwischen den Mittelwerten (μ₁ - μ₂) lautet:

CI = (x̄₁ - x̄₂) ± Z√[(s₁²/n₁) + (s₂²/n₂)]

Wobei:

• x̄₁ und x̄₂ sind die Stichprobenmittelwerte der beiden Gruppen.
• s₁ und s₂ sind die Stichprobenstandardabweichungen der beiden Gruppen.
• n₁ und n₂ sind die Stichprobengrößen der beiden Gruppen.
• Z ist der kritische Wert aus der Standardnormalverteilung, der dem gewünschten Konfidenzniveau entspricht.

Beispiel:

Betrachten wir eine Studie, in der die Wirksamkeit von zwei Programmen zur Gewichtsreduktion verglichen wird. Eine Stichprobe von 50 Teilnehmern wird nach dem Zufallsprinzip jedem Programm zugewiesen, und ihr Gewichtsverlust in Pfund nach sechs Monaten wird aufgezeichnet. Nehmen wir an, der mittlere Gewichtsverlust der Stichprobe für Programm A beträgt 12 Pfund mit einer Standardabweichung von 3 Pfund, während er für Programm B 10 Pfund mit einer Standardabweichung von 2 Pfund beträgt. Um ein 99%-Konfidenzintervall für den Unterschied im mittleren Gewichtsverlust zwischen den beiden Programmen zu konstruieren, können wir die Formel verwenden:

CI = (12 - 10) ± 2.576√[(3²/50) + (2²/50)]

CI = 2 ± 1,63

Das 99%ige Konfidenzintervall für den Unterschied im mittleren Gewichtsverlust zwischen Programm A und Programm B beträgt also etwa 0,37 bis 3,63 Pfund.

Konfidenzintervall für die Differenz zwischen den Proportionen

In ähnlicher Weise wird das Konfidenzintervall für die Differenz zwischen Proportionen verwendet, wenn die Proportionen zweier Populationen oder Gruppen verglichen werden, z. B. die Erfolgsquoten zweier Behandlungen.

Formel für das Konfidenzintervall für die Differenz zwischen den Anteilen

Die Formel zur Berechnung des Konfidenzintervalls für die Differenz zwischen den Anteilen (p₁ - p₂) lautet:

CI = (p̂₁ - p̂₂) ± Z√[(p̂₁(1-p̂₁)/n₁) + (p̂₂(1-p̂₂)/n₂)]

Wobei:

• p̂₁ und p̂₂ sind die Stichprobenanteile der beiden Gruppen.
• n₁ und n₂ sind die Stichprobengrößen der beiden Gruppen.
• Z ist der kritische Wert aus der Standardnormalverteilung, der dem gewünschten Konfidenzniveau entspricht.

Beispiel:

Angenommen, wir führen eine klinische Studie durch, um die Wirksamkeit von zwei Medikamenten bei der Behandlung einer bestimmten Erkrankung zu vergleichen. In Gruppe 1 zeigen von einer Stichprobe von 200 Patienten 140 eine Verbesserung. In Gruppe 2 zeigen von einer Stichprobe von 250 Patienten 150 eine Besserung. Um ein 95 %-Konfidenzintervall für den Unterschied in den Anteilen der Patienten, die eine Verbesserung zwischen den beiden Gruppen zeigen, zu konstruieren, können wir die Formel verwenden:

CI = [(140/200) - (150/250)] ± 1,96√[((140/200)(1-(140/200))/200) + ((150/250)(1-(150/250))/250)]

CI = (0,70 - 0,60) ± 0,087

Das 95 %-Konfidenzintervall für den Unterschied in den Anteilen der Patienten, die eine Verbesserung zwischen den beiden Gruppen aufweisen, beträgt also etwa 0,01 bis 0,19.

Wenn Forscher die verschiedenen Arten von Konfidenzintervallen und ihre jeweiligen Formeln kennen, können sie Daten aus verschiedenen Populationen oder Gruppen effektiv analysieren und vergleichen, was zu einer fundierten Entscheidungsfindung und robusten statistischen Schlussfolgerungen führt.

Wie konstruiert man ein Konfidenzintervall?

Die Berechnung von Konfidenzintervallen erfordert die sorgfältige Berücksichtigung verschiedener Faktoren, vom Stichprobenumfang bis zur Wahl der statistischen Methode. Im Folgenden finden Sie einige praktische Tipps, die Ihnen helfen, Konfidenzintervalle genau zu berechnen.

1. Verstehen Sie Ihre Daten: Bevor Sie Konfidenzintervalle berechnen, sollten Sie Ihre Daten und die Studienpopulation genau verstehen. Berücksichtigen Sie Faktoren wie die Datenverteilung, den Stichprobenumfang und die Art der Grundgesamtheit.
2. Wählen Sie die richtige Formel: Wählen Sie die geeignete Formel für die Berechnung von Konfidenzintervallen auf der Grundlage der Merkmale Ihrer Daten, z. B. des Stichprobenumfangs und der Tatsache, ob die Standardabweichung der Grundgesamtheit bekannt ist.
3. Überprüfen Sie die Annahmen: Überprüfen Sie die Gültigkeit der Annahmen, die der Berechnung der Konfidenzintervalle zugrunde liegen, wie z. B. die Normalität der Daten und die Unabhängigkeit der Beobachtungen. Ein Verstoß gegen diese Annahmen kann zu ungenauen Ergebnissen führen.
4. Verwenden Sie Software oder Online-Rechner: Es ist zwar wichtig, die der Berechnung von Konfidenzintervallen zugrunde liegenden Prinzipien zu verstehen, aber die Verwendung von Software oder Online-Rechnern kann den Prozess rationalisieren und die Wahrscheinlichkeit von Berechnungsfehlern verringern.
5. Prüfen Sie auf Ausreißer: Ausreißer können die Ergebnisse von Konfidenzintervallen erheblich beeinflussen. Prüfen Sie vor der Berechnung der Intervalle auf Ausreißer und überlegen Sie, ob diese entfernt oder in der Analyse berücksichtigt werden sollten.
6. Interpretieren Sie die Ergebnisse mit Vorsicht: Denken Sie bei der Interpretation von Konfidenzintervallen daran, dass sie Schätzungen mit einem gewissen Grad an Unsicherheit liefern. Vermeiden Sie es, enge Intervalle zu überinterpretieren oder allein aufgrund der Intervallgrenzen endgültige Schlussfolgerungen zu ziehen.
7. Berücksichtigen Sie die praktische Signifikanz: Berücksichtigen Sie neben der statistischen Bedeutung auch die praktische Bedeutung Ihrer Ergebnisse. Ein statistisch signifikanter Unterschied ist nicht immer auch praktisch signifikant. Berücksichtigen Sie den Kontext und die Implikationen Ihrer Ergebnisse.

Konfidenzintervall-Anwendungen

Konfidenzintervalle sind nicht nur theoretische Konstrukte, sondern finden in verschiedenen Bereichen praktische Anwendung, von der Gesundheitsfürsorge über das Finanzwesen bis hin zur Forschung und anderen Bereichen.

Beispiele aus der Praxis für die Verwendung von Konfidenzintervallen

1. Medizinische Forschung: In klinischen Studien werden Konfidenzintervalle verwendet, um die Wirksamkeit neuer Behandlungen im Vergleich zu bestehenden Behandlungen abzuschätzen. So können Forscher beispielsweise Konfidenzintervalle verwenden, um festzustellen, ob ein neues Medikament im Vergleich zu einem Placebo oder einer Standardbehandlung zu einer signifikanten Verringerung der Symptome führt.
2. Marktforschung: Unternehmen führen häufig Umfragen durch, um Erkenntnisse über die Präferenzen und das Verhalten der Verbraucher zu gewinnen. Konfidenzintervalle helfen bei der Schätzung von Parametern wie der Kundenzufriedenheit oder dem Marktanteil und liefern verwertbare Erkenntnisse für Marketingstrategien und Produktentwicklung.
3. Wirtschaftliche Analyse: Wirtschaftswissenschaftler verwenden Konfidenzintervalle, um wichtige Wirtschaftsindikatoren wie Arbeitslosenquoten oder Inflationsraten zu schätzen. Diese Schätzungen dienen politischen Entscheidungsträgern als Entscheidungshilfe für geldpolitische Maßnahmen und wirtschaftliche Anreize.
4. Qualitätskontrolle: Hersteller verwenden Konfidenzintervalle, um die Qualität ihrer Produkte und Prozesse zu überwachen. Ein Produktionsleiter könnte beispielsweise Konfidenzintervalle verwenden, um die Fehlerquote in einem Fertigungsprozess zu schätzen und Anpassungen zur Verbesserung der Produktqualität vorzunehmen.
5. Umweltwissenschaft: Umweltwissenschaftler verwenden Konfidenzintervalle zur Schätzung von Populationsparametern im Zusammenhang mit Umweltfaktoren, wie z. B. Luftqualität oder Wasserverschmutzung. Diese Schätzungen dienen politischen Entscheidungsträgern und Aufsichtsbehörden als Grundlage für die Umsetzung von Maßnahmen zum Schutz der öffentlichen Gesundheit und der Umwelt.

Konfidenzintervalle Herausforderungen

Konfidenzintervalle sind ein leistungsfähiges Instrument, das jedoch bei unsachgemäßer Anwendung mit verschiedenen Fehlern und Fallstricken behaftet sein kann. Wenn Sie sich dieser häufigen Fehler bewusst sind, können Sie die Genauigkeit und Zuverlässigkeit Ihrer Analysen sicherstellen. Hier sind einige häufige Probleme, auf die Sie achten sollten.

• Fehlinterpretation des Konfidenzniveaus: Ein häufiger Fehler ist die Fehlinterpretation des Konfidenzniveaus. Ein Konfidenzniveau von 95 % bedeutet nicht, dass eine Wahrscheinlichkeit von 95 % besteht, dass der wahre Parameter innerhalb des Intervalls liegt. Vielmehr bedeutet es, dass bei einer mehrfachen Wiederholung des Stichprobenverfahrens 95 % der sich ergebenden Intervalle den wahren Parameter enthalten würden.
• Ignorieren von Annahmen: Konfidenzintervalle beruhen auf bestimmten Annahmen, z. B. der Normalität der Daten oder der Unabhängigkeit der Beobachtungen. Die Nichtbeachtung dieser Annahmen kann zu ungenauen Ergebnissen führen. Vor der Anwendung von Konfidenzintervallen ist es wichtig, die Gültigkeit der Annahmen zu überprüfen.
• Kleine Stichprobengrößen: Konfidenzintervalle werden mit kleineren Stichprobenumfängen weniger zuverlässig. Kleine Stichproben können zu breiteren Intervallen und weniger präzisen Schätzungen der Populationsparameter führen. Seien Sie vorsichtig bei der Interpretation von Konfidenzintervallen aus kleinen Stichproben und erwägen Sie, den Stichprobenumfang nach Möglichkeit zu erhöhen.
• Nicht-repräsentative Stichproben: Die Verwendung nicht repräsentativer Stichproben kann die Konfidenzintervalle verfälschen. Stellen Sie sicher, dass Ihre Stichprobe repräsentativ für die interessierende Population ist, um genaue Schätzungen zu erhalten. Verzerrte Stichproben können zu Konfidenzintervallen führen, die nicht den wahren Populationsparameter widerspiegeln.
• Falsche Formelauswahl: Verschiedene Szenarien erfordern unterschiedliche Formeln für die Berechnung von Konfidenzintervallen. Die Verwendung der falschen Formel, z. B. die Verwendung des z-Tests anstelle des t-Tests für kleine Stichprobengrößen, kann zu falschen Intervallen führen. Wählen Sie stets die geeignete Formel auf der Grundlage der Merkmale Ihrer Daten.
• Verwechslung von Präzision und Genauigkeit: Ein engeres Konfidenzintervall bedeutet nicht unbedingt eine höhere Genauigkeit. Es spiegelt eine größere Präzision bei der Schätzung des Parameters wider, ist aber keine Garantie dafür, dass die Schätzung genau ist. Berücksichtigen Sie bei der Interpretation von Konfidenzintervallen sowohl Präzision als auch Genauigkeit.
• Mehrfache Vergleiche: Die Durchführung von Mehrfachvergleichen ohne Anpassung an die Multiplizität kann die Gesamtfehlerrate vom Typ I erhöhen. Seien Sie bei der Interpretation von Konfidenzintervallen aus Mehrfachvergleichen vorsichtig und ziehen Sie eine Anpassung für die Multiplizität mit Methoden wie der Bonferroni-Korrektur in Betracht.

Fortgeschrittene Themen zu Konfidenzintervallen

Konfidenzintervalle gehen über traditionelle Methoden wie den z-Test oder t-Test hinaus. Fortgeschrittene Techniken bieten mehr Flexibilität und Robustheit bei der Schätzung von Populationsparametern. Im Folgenden werden einige dieser fortgeschrittenen Themen der Konfidenzintervallschätzung untersucht.

Bootstrap-Methode zur Berechnung von Konfidenzintervallen

Die Bootstrap-Methode ist ein Wiederholungsstichprobenverfahren, das einen alternativen Ansatz zur Berechnung von Konfidenzintervallen bietet, insbesondere wenn die zugrunde liegenden Annahmen parametrischer Methoden verletzt werden. Anstatt sich auf theoretische Verteilungen zu stützen, werden beim Bootstrap-Resampling mehrere Stichproben aus den beobachteten Daten gezogen, um die Stichprobenverteilung einer Statistik empirisch zu schätzen.

Verfahren für die Bootstrap-Methode:

1. Wiederholungsstichproben: Erzeugen einer großen Anzahl von Bootstrap-Stichproben durch zufällige Stichproben mit Ersetzung aus den beobachteten Daten.
2. Berechnen Sie die Statistik: Berechnen Sie für jede Bootstrap-Stichprobe die betreffende Statistik (z. B. Mittelwert, Median, Anteil).
3. Schätzen Sie die Verteilung: Konstruieren Sie die Stichprobenverteilung der Statistik auf der Grundlage der Bootstrap-Wiederholungen.
4. Berechnen Sie das Konfidenzintervall: Bestimmen Sie das Konfidenzintervall, indem Sie den entsprechenden Perzentilbereich aus der Stichprobenverteilung erhalten.

Vorteile der Bootstrap-Methode:

• Verteilungsfrei: Die Bootstrap-Methode beruht nicht auf Annahmen über die zugrundeliegende Verteilung der Daten und ist daher für nicht-parametrische oder komplexe Datenstrukturen geeignet.
• Flexibel: Die Bootstrap-Methode kann auf eine Vielzahl von statistischen Schätzern und Hypothesentests angewendet werden und bietet somit Flexibilität bei der Analyse.
• Robustheit: Bootstrap-Konfidenzintervalle sind robust gegenüber Verletzungen der Normalität und anderer Annahmen und liefern zuverlässigere Schätzungen in realen Szenarien.

Bayesscher Ansatz für Konfidenzintervalle

In der Bayes'schen Statistik werden Konfidenzintervalle durch Glaubwürdigkeitsintervalle ersetzt, die die Unsicherheit von Parameterschätzungen aus einer Bayes'schen Perspektive widerspiegeln. Im Gegensatz zu den frequentistischen Konfidenzintervallen, die einen Bereich plausibler Werte auf der Grundlage der Stichprobenvariabilität liefern, berücksichtigen die Bayes'schen Konfidenzintervalle vorherige Informationen und aktualisieren die Überzeugungen auf der Grundlage der beobachteten Daten unter Verwendung des Bayes'schen Theorems.

Verfahren für den Bayes'schen Ansatz:

1. Prior-Verteilung spezifizieren: Definieren Sie eine Vorabverteilung, die das vorhandene Wissen oder die Überzeugungen über den interessierenden Parameter repräsentiert, bevor die Daten beobachtet werden.
2. Mit Daten aktualisieren: Verwenden Sie das Bayes-Theorem, um die Prior-Verteilung auf der Grundlage der Likelihood-Funktion der beobachteten Daten zu aktualisieren, was zur Posterior-Verteilung führt.
3. Glaubwürdiges Intervall konstruieren: Ermitteln Sie das glaubwürdige Intervall, indem Sie den Bereich der Posterior-Verteilung auswählen, der eine bestimmte Wahrscheinlichkeitsmasse enthält (z. B. 95 %).

Vorteile des Bayes'schen Ansatzes:

• Einbeziehung von Vorinformationen: Bayes'sche Glaubwürdigkeitsintervalle ermöglichen die Einbeziehung von Vorannahmen oder Expertenwissen über den Parameter, was zu informativeren Schlussfolgerungen führt.
• Flexibilität: Bayes'sche Methoden können mit komplexen Modellen und hierarchischen Strukturen umgehen und eignen sich daher für ein breites Spektrum statistischer Probleme.
• Probabilistische Interpretation: Glaubwürdige Intervalle haben eine einfache probabilistische Interpretation, die die Unsicherheit in den Parameterschätzungen in Anbetracht der beobachteten Daten und der vorherigen Informationen darstellt.

Nichtparametrische Methoden

Nichtparametrische Methoden bieten Alternativen zu den traditionellen parametrischen Ansätzen, da sie weniger Annahmen über die zugrunde liegende Verteilung der Daten machen. Diese Methoden sind besonders nützlich, wenn es sich um Daten handelt, die keiner bestimmten Verteilung folgen, oder wenn der Stichprobenumfang gering ist.

Beispiele für nichtparametrische Methoden:

• Bootstrap-Methode: Wie bereits erwähnt, ist die Bootstrap-Methode eine vielseitige nichtparametrische Technik zur Schätzung von Konfidenzintervallen, ohne dass eine bestimmte Verteilung angenommen wird.
• Rang-basierte Methoden: Rangbasierte Verfahren, wie der Wilcoxon-Rangsummentest oder der Mann-Whitney-U-Test, verwenden die Ränge der Beobachtungen und nicht die tatsächlichen Datenwerte, was sie robust gegenüber Nicht-Normalität und Ausreißern macht.
• Permutationstests: Bei Permutationstests werden die Beobachtungen nach dem Zufallsprinzip zwischen den Gruppen umverteilt, um eine Nullverteilung zu erzeugen, so dass Hypothesentests und Konfidenzintervallschätzungen möglich sind, ohne dass eine bestimmte Verteilung angenommen wird.

Nicht-parametrische Methoden bieten Flexibilität und Robustheit in Situationen, in denen parametrische Annahmen verletzt werden, oder wenn es um komplexe Datenstrukturen geht. Durch den Einsatz dieser fortschrittlichen Techniken können Forscher zuverlässigere und informativere Konfidenzintervalle für ihre Analysen erhalten.

Fazit zu Konfidenzintervallen

Konfidenzintervalle sind in der statistischen Analyse von unschätzbarem Wert, da sie eine präzise Schätzung von Populationsparametern und eine Bewertung der Unsicherheit unserer Schätzungen ermöglichen. Da Konfidenzintervalle einen Bereich plausibler Werte zusammen mit einem Maß für das Vertrauen liefern, können Forscher, Entscheidungsträger und Praktiker fundierte Entscheidungen auf der Grundlage empirischer Belege treffen. Ganz gleich, ob es darum geht, die Wirksamkeit einer neuen Behandlung zu bestimmen, Markttrends abzuschätzen oder die Auswirkungen politischer Maßnahmen zu bewerten - Konfidenzintervalle bieten einen zuverlässigen Rahmen, um aus Stichprobendaten Schlussfolgerungen zu ziehen und Handlungen mit Zuversicht anzuleiten.

Bei der weiteren Anwendung von Konfidenzintervallen in Ihrer eigenen Arbeit sollten Sie die zugrundeliegenden Annahmen verstehen, geeignete Berechnungsmethoden wählen und die Ergebnisse mit Vorsicht interpretieren. Indem Sie bewährte Verfahren einbeziehen und bei Bedarf fortschrittliche Techniken einsetzen, können Sie die Leistungsfähigkeit von Konfidenzintervallen nutzen, um aussagekräftige Erkenntnisse zu gewinnen, eine evidenzbasierte Entscheidungsfindung zu unterstützen und zu Fortschritten in Ihrem Bereich beizutragen.

Wie führt man statistische Forschung in wenigen Minuten durch?

Wir stellen Ihnen Appinio vor, die Echtzeit-Marktforschungsplattform, die die Art und Weise revolutioniert, wie Unternehmen Erkenntnisse über Verbraucher gewinnen. Mit Appinio ist die Durchführung Ihrer eigenen Marktforschung ein Kinderspiel. Verabschieden Sie sich von langwierigen Datenerfassungsprozessen und freuen Sie sich auf sofortige Erkenntnisse.

Hier erfahren Sie, warum Appinio Ihre erste Wahl für schnelle und zuverlässige Marktforschung ist:

• Von Fragen zu Erkenntnissen in wenigen Minuten: Mit unserer Plattform können Sie innerhalb weniger Minuten von der Formulierung Ihrer Forschungsfragen zu verwertbaren Erkenntnissen gelangen. Sie müssen nicht mehr Tage oder Wochen auf Ergebnisse warten.
• Intuitive Plattform für jedermann: Sie brauchen keinen Doktortitel in Forschung, um Appinio zu nutzen. Unsere Plattform ist so konzipiert, dass sie intuitiv und benutzerfreundlich ist, so dass jeder sie leicht bedienen und wie ein Profi recherchieren kann.
• Schnelle Durchlaufzeit: Sie brauchen schnell Antworten? Mit einer durchschnittlichen Feldzeit von weniger als 23 Minuten für 1.000 Befragte liefert Appinio schnell Ergebnisse und ermöglicht es Ihnen, in Rekordzeit fundierte Entscheidungen zu treffen.

Kostenlos registrieren

Kostenlosen Zugang zur Appinio Platform erhalten!

Or

Continue with Google Continue with Microsoft